How To Find The Perimeter Of A Rectangle: A Comprehensive Guide

Haley Leannon 11 Aug 2025

Calculating the perimeter of a rectangle is a fundamental concept in mathematics that plays a crucial role in various real-life applications. Whether you're a student learning geometry, a professional working on construction projects, or simply someone interested in understanding the basics of measurements, mastering this skill is essential. By the end of this article, you'll have a thorough understanding of how to find the perimeter of a rectangle and its practical applications.

Rectangles are one of the most common shapes we encounter in our daily lives, from the screens of our devices to the walls of our homes. Understanding how to calculate the perimeter of a rectangle is not only important for academic purposes but also for practical situations like planning a garden, designing a room layout, or even estimating material costs for a project.

This guide will take you through the step-by-step process of calculating the perimeter of a rectangle, along with tips, examples, and real-world applications. We'll also explore related concepts to give you a well-rounded understanding of the topic. Let's dive in!

1. What is Perimeter?

2. Formula for Finding the Perimeter of a Rectangle

3. Step-by-Step Guide to Calculate the Perimeter of a Rectangle

4. Common Mistakes to Avoid When Finding the Perimeter

5. Practical Examples of Calculating the Perimeter

6. Real-World Applications of Rectangle Perimeters

7. Advanced Concepts Related to Rectangle Perimeters

8. Tips and Tricks for Mastering Perimeter Calculations

9. Frequently Asked Questions About Rectangle Perimeters

10. Conclusion

What is Perimeter?

The term "perimeter" refers to the total distance around the edge of a two-dimensional shape. In simpler terms, it is the sum of all the sides of a shape. For a rectangle, the perimeter is calculated by adding the lengths of all four sides. Understanding what perimeter means is essential before diving into the specifics of how to calculate it for a rectangle.

Perimeter is expressed in linear units such as meters, feet, inches, or centimeters. It is a fundamental concept in geometry and has numerous applications in fields like engineering, architecture, and design. Whether you're measuring the boundary of a field, designing a room, or planning a construction project, knowing how to calculate the perimeter is invaluable.

Why is Perimeter Important?

Perimeter calculations are not just limited to academic settings. They play a significant role in everyday life. For instance, if you're planning to install fencing around your property, knowing the perimeter will help you estimate the amount of material needed. Similarly, in interior design, calculating the perimeter can help determine the amount of trim or baseboard required for a room.

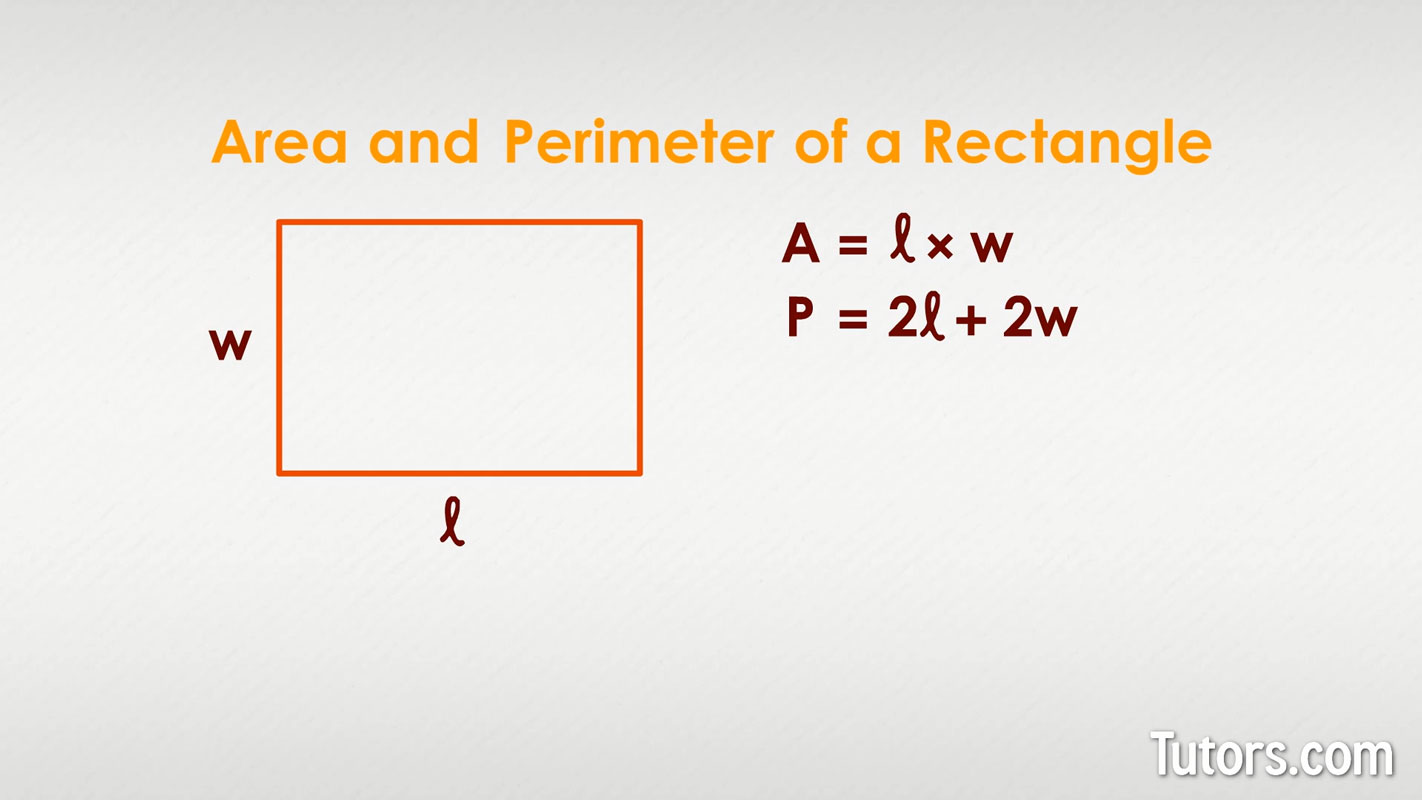
Formula for Finding the Perimeter of a Rectangle

The formula for finding the perimeter of a rectangle is straightforward: \( P = 2(l + w) \), where \( P \) represents the perimeter, \( l \) is the length, and \( w \) is the width of the rectangle. This formula accounts for the fact that opposite sides of a rectangle are equal in length, making it easier to calculate the total distance around the shape.

Breaking Down the Formula

\( l \): The longer side of the rectangle (length).
\( w \): The shorter side of the rectangle (width).
Adding the length and width, then multiplying by 2, gives the total perimeter.

For example, if a rectangle has a length of 10 meters and a width of 5 meters, the perimeter would be \( P = 2(10 + 5) = 30 \) meters.

Step-by-Step Guide to Calculate the Perimeter of a Rectangle

Now that you understand the formula, let's break down the process into simple steps:

Identify the length (\( l \)) and width (\( w \)) of the rectangle.
Add the length and width together: \( l + w \).
Multiply the sum by 2 to get the perimeter: \( 2(l + w) \).
Ensure your final answer is in the correct unit of measurement.

Let's apply this process to an example. Suppose you have a rectangle with a length of 8 feet and a width of 4 feet:

Add the length and width: \( 8 + 4 = 12 \).
Multiply by 2: \( 2 \times 12 = 24 \).
The perimeter is 24 feet.

Common Mistakes to Avoid When Finding the Perimeter

While calculating the perimeter of a rectangle is relatively simple, there are a few common mistakes that people often make. Here are some pitfalls to watch out for:

Confusing length and width: Always double-check which side is the length and which is the width.
Forgetting to multiply by 2: The formula requires you to multiply the sum of the length and width by 2, so don't skip this step.
Using inconsistent units: Ensure all measurements are in the same unit before performing calculations.

By being aware of these potential errors, you can avoid them and ensure accurate results.

Practical Examples of Calculating the Perimeter

Let's explore a few practical examples to solidify your understanding:

Example 1: Garden Fence

Suppose you want to build a fence around a rectangular garden that measures 15 meters in length and 10 meters in width. Using the formula \( P = 2(l + w) \), the perimeter would be:

\( P = 2(15 + 10) = 2(25) = 50 \) meters.

You would need 50 meters of fencing material to enclose the garden.

Example 2: Room Layout

If you're designing a room that is 12 feet long and 8 feet wide, the perimeter would be:

\( P = 2(12 + 8) = 2(20) = 40 \) feet.

This information can help you plan the placement of furniture or estimate the amount of baseboard needed.

Real-World Applications of Rectangle Perimeters

Understanding how to calculate the perimeter of a rectangle has numerous real-world applications:

Construction: Architects and builders use perimeter calculations to determine the amount of materials needed for projects like fencing, roofing, and flooring.
Agriculture: Farmers use perimeter measurements to plan irrigation systems and estimate the amount of fencing required for fields.
Interior Design: Designers use perimeter calculations to plan room layouts, determine the amount of trim needed, and estimate material costs.

These applications highlight the importance of mastering this fundamental concept.

Advanced Concepts Related to Rectangle Perimeters

Once you've mastered the basics, you can explore more advanced concepts related to rectangle perimeters:

Perimeter and Area

While perimeter measures the distance around a shape, area measures the space inside it. For a rectangle, the area is calculated using the formula \( A = l \times w \). Understanding the relationship between perimeter and area can help solve more complex problems.

Irregular Shapes

Some real-world objects may not have perfect rectangular shapes. In such cases, you can break the shape into smaller rectangles and calculate their individual perimeters to find the total.

Tips and Tricks for Mastering Perimeter Calculations

Here are some tips to help you become more proficient in calculating rectangle perimeters:

Practice Regularly: The more you practice, the more comfortable you'll become with the calculations.
Use Visual Aids: Drawing diagrams can help visualize the problem and make calculations easier.
Double-Check Your Work: Always verify your calculations to ensure accuracy.

Frequently Asked Questions About Rectangle Perimeters

Here are some common questions people have about calculating rectangle perimeters:

Q: What happens if the rectangle is a square?

A: If the rectangle is a square, all sides are equal, so the formula simplifies to \( P = 4s \), where \( s \) is the side length.

Q: Can perimeter calculations be applied to three-dimensional objects?

A: Perimeter calculations are typically used for two-dimensional shapes. For three-dimensional objects, you would calculate the surface area or volume instead.

Conclusion

In conclusion, learning how to find the perimeter of a rectangle is a valuable skill with numerous practical applications. By understanding the formula \( P = 2(l + w) \) and practicing regularly, you can master this concept and apply it to various real-world scenarios. Remember to avoid common mistakes, use visual aids, and double-check your work for accuracy.

We encourage you to share this article with others who might find it helpful and explore more resources on our website. If you have any questions or comments, feel free to leave them below. Happy calculating!

Perimeter Of Rectangle Definition, Formula Examples, 56 OFF

How to Find the perimeter of a rectangle « Math WonderHowTo

How to Find the Perimeter of a Rectangle « Math

NewsCrafter